Mosaic

Posted

I recently opened a new repository here, which an sich consists more or less of a single, chaotic script - but there is come conceptual content, so I thought I would write something down before forgetting about it.

The idea for the script was simple: divide an image in square tiles, then, given a list of mosaic tiles on the market, find for each tile in which the picture has been divided the most suitable tile on the market to represent it. So the script produces a first suggestion on how to construct a mosaic starting from any given image and number of tiles, and you can then build on that. Sounds good, right?

The non intuitive part is in fact formally defining “most suitable”. The naïve attempt at finding the most suitable tile could go like this:

  1. Realize that every colour is a three dimensional vector (RGB);
  2. Average the three components over the image tile to obtain a single vector representing it;
  3. Select the mosaic tile for which the norm of the difference between the vector representing the mosaic tile and the vector representing the image tile is minimal.

The fascinating fact is that this fails spectacularly, for the simple reason that the Euclidean norm is not the right norm for the RGB space (from the human eye’s, well, point of view), for whatever reasons. The problem of finding the right norm is not really easy, but luckily the question is general enough that somebody else already thought about it and found a good solution, so that you don’t need to worry too much about it.

What I found amusing about the solution is that it does not consist in providing the right norm, but rather in moving around every vector so that the Euclidean distance between the shifted vectors equals the correct distance for the unshifted vectors. I was working with this source image:

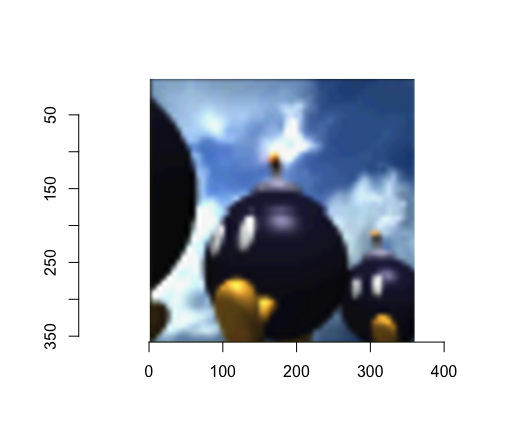Source Which shifts to this:

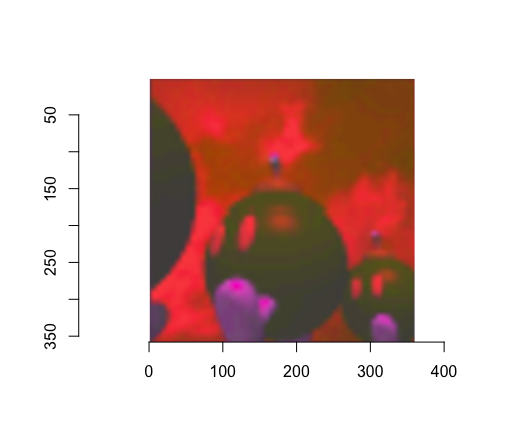Shifted So the plan is of course to take the image, shift it, tile it, then shift it back. Clockwise, starting up left:

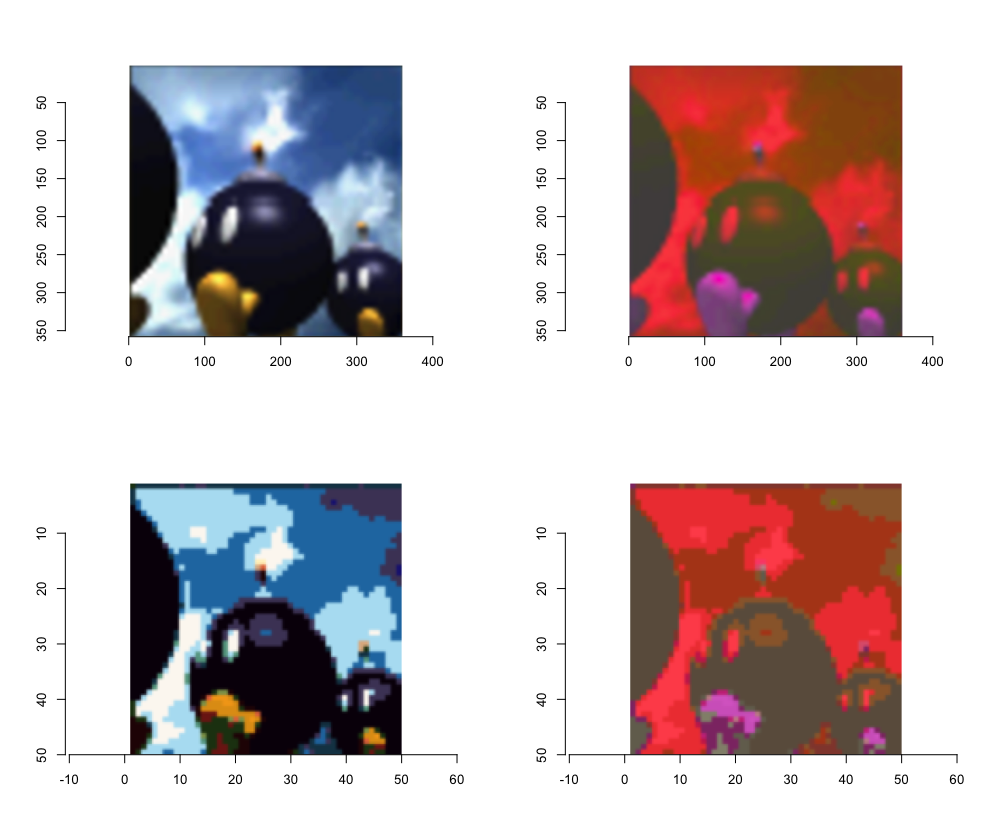Process Here’s a comparison between the output just presented and the one obtained following the naïve approach: